Understanding Plasma, Part 2: Make Plasma Fungible Again

Quick Take
- Scaling Ethereum is an unprecedented challenge, Plasma is a Layer 2 scaling framework that aims to increase transaction throughput
- Part 2 addresses checkpoints, proof compression, merkle trees, and more
This article is the second entry of a multi-part series explaining Plasma, by Daniel Goldman.

Previously on "Understanding Plasma"
[related id="1"]In Part 1, we kicked off the Plasma research journey, the quest for a high-throughput payment system that retains the security of the Ethereum chain with only occasional, constant-size on-chain transactions. We left off at the Plasma Cash construction, which gave us many of the features we sought, though brought with it two big downsides: Plasma Cash "coins" are effectively non-fungible tokens (restricting the flexibility of payment denominations), and it requires users to store a large, ever-growing data-set.
Here, we'll explore some additional features and mechanisms that build on top of Plasma Cash (and/or rethink it) designed to circumvent — or at least mitigate —these downsides.
Some up-front disclaimers: Things will get complicated. To steal a metaphor from mathematician Peter Saran, research of this sort can start to feel like trying to flatten a carpet with dimensions slightly larger than the room it resides in; step on one corner, and another section unexpectedly pops up. Additionally, this will start to approach the event horizon of Plasma research; as we'll see, some questions are still up in the air, and much of what's discussed here is still being explored, with further developments and discoveries constantly taking place.
With that, onward:
Less Client-Side Data, Strategy 1: Checkpoints
What we saw in (what we'll hereby refer to as) Vanilla Plasma Cash was that the amount of data each client needs to store grows linearly over time; i.e., for each coin, one Merkle proof of either inclusion (coin was spent) or exclusion (coin stayed put) is required for every Plasma block. This full history is necessary, because there’s no telling which piece of it a user may need to settle a dispute. Storing all of this data is a pain, and transferring all of it to the next owner every time a payment is made even more so.
To help ease this pain, imagine if at some regular intervals — every two weeks, or every 500 Plasma blocks, say — some "On Chain Thing" happens that officially establishes the ownership of some (or all) of the Plasma Cash coins. The idea is, once this "On Chain Thing" is finalized, it would serve as a historical checkpoint: future proofs of ownership now only have to go back as far as this point; no disputes involving any prior history are allowed. Thus, the Merkle proofs of all prior blocks can be safely discarded for good. This would put a concrete upper-bound on the size of the requisite client-side data. Big win.
The first thing we need to make these checkpoints work is a way for the Plasma operator (or anyone else, but we'll assume the operator for simplicity) to attest to the full state of coin ownership at a given Plasma block. As you may have well guessed by now, this will involve a Merkle Tree: the operator constructs a tree that simply maps each coin to its owners address and then sends the Merkle root to the mainchain; each owner receives their corresponding Merkle branch; if, after 2 weeks (or whatever) this all goes unchallenged, we consider this checkpointed state official. (This does require each user to be online to receive this data and monitor the chain, but recall that for Plasma, as with any layer 2 construction, this liveness is required anyway.)
Are we all set then? Alas, life isn't so simple. Unfortunately, the checkpoint mechanism as described above introduces a pretty nasty edge-case. Suppose a malicious/compromised/bored operator broadcasts the Merkle root for a checkpoint, but then fails to share any of the Merkle proof data with the users. Now what? Any approach that lets users force the operator to provide this data brings us into speaker-listener fault equivalence territory, with the usual griefing vectors & complications abound. We could point out that users still have the option to safely withdraw their funds back onto the mainchain, which is technically true. But the problem is, now every user would have to stampede onto the mainchain, and they would have to do so within some bounded, two-week window because of the checkpoints we just introduced. The "mass-exit" corner of the carpet we so cleverly pressed down in part 1 pops up again.
But all is not lost; we can save things with an additional bit of work in the form of "Cryptoeconomic Aggregate Signatures" (less intimidating than it sounds, I promise). In essence, we modify the ownership-attestation slightly such that the operator requires the signature of each coin's owner in the checkpoint; in other words, the operator can only checkpoint a coin with its owner's explicit consent. The operator then also posts some additional data on chain: an attestation of which coins are included in the checkpoint (imagine each coin represented in a list of binary digits, with a "1" signifying consent/inclusion and a "0" exclusion.)
Counterintuitive though it may seem, this is enough to solve things! The key observation here is that each coin has some valid owner; that owner knows who they are, and likewise, they know whether or not they consented to a given checkpoint. Thus, the only case they need to worry about is the one in which they didn't sign off on checkpointing one of their coins, but still see a "1" in the coin's slot. In this case, they simply challenge — a challenge which they know will succeed — and invalidate the checkpoint. Mass exits avoided, checkpoints safe and sound.
Layer 2 purists will be quick to note here that the on-chain requirement here is not a "strictly-Plasma" approach; the size of the bitmap data is linearly correlated to the number of coins. Pragmatically speaking, however, this cost should be fairly minimal, especially since in most cases the data can probably be drastically reduced with simple bit-field compression techniques. Plus, a checkpoint benefits all of the coins it notarizes, so the cost of the on-chain transaction would ideally be amortized among all of the coin’s owners. Add to all of this the fact that checkpointing is voluntary, and it's ultimately (arguably) a pretty concrete win.
Less Client-Side Data, Strategy 2: Proof Compression
A different, more advanced approach for minimizing storage requirements is to effectively compress many Plasma block proofs down into one. Again, recall that for a Vanilla Plasma Cash coin, one exclusion or inclusion Merkle proof per block is required. The idea now is to add a requirement for inclusion: not only do we require the on-chain Merkle root and off-chain Merkle branch, we also require an on-chain “RSA accumulator,” (a secondary way of proving membership using pure number theory) and an off-chain “proof of knowledge” (details explained shortly, just roll with it for now). Since both of these are required to prove inclusion, only one is required to prove exclusion; i.e., a coin is either included in a block or it isn't; there are no other possibilities, and the negation of “Both A and B (for inclusion)” is “Either A or B (for exclusion)”.
On a high level, this construction is taking advantage of the fact that exclusion is an inherently simpler thing to attest to; if a coin is included, we need some more data — namely, the address of its new recipient at the very least. Whereas in the exclusion case, the statement “this coin isn't included" is all there is to say. It stands to reason that we should be able to exploit this asymmetry with a less burdensome commitment scheme for the exclusion case.
(Warning: math incoming)
With simplifications abound, here's how it works: as is the usual Plasma Cash M.O., each coin will get assigned an ID in the form of a natural number, but now we'll impose the additional requirement that all of these IDs are prime numbers. The RSA accumulator (G) that gets committed with each Plasma block is itself just a number; it updates with every Plasma block according to the coins that were transferred.
In essence, G gets raised to the power of each spent coin’s ID in the current block. Say, for example, in block 101, coins with IDs of 5, 7, 17, 53, and 83 were transferred (all prime numbers, #Don'tTrustVerify). Let's call the accumulator value committed in the 100th block G₁₀₀ (some big number); the accumulator value for block 101 is computed as follows:
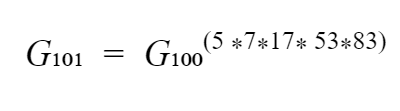
This new G₁₀₁value gets committed to the mainchain.
In off-chain, layer 2 world, for Alice (who, let's say, owns the "17" coin) to get assurance that her coin is committed in the accumulator, she only needs 17’s cofactor in the exponent — 5*7*53*83 (which is 153,965. incidentally). She acquires G₁₀₁ and G₁₀₁on the mainchain, and verifies for herself that:
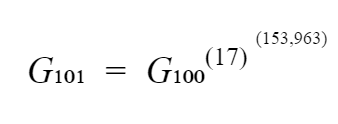
This confirms that her coin's number, 17 was absorbed into the accumulator. She also gets the usual Merkle branch commitment; once she confirms this as well, she's all set.
Now let's consider Bob, the owner of coin with ID 11, a coin which, notice, was not transferred in block 101. To get his proof of absence, Bob gets proof that his number, 11, is not a factor of 153,965. For this, he just needs a cofactor to show that 11 is a factor of some number close to 5 * 7 * 17 * 53 by less than 11. Again, all he needs, essentially, is a single number. Once he has this he's done; again, given the “either/or” nature of our requirements, proof of exclusion doesn't require Bob to worry about any of the Merkle-branch business at all.
And here, finally, is the key: given the properties of exponentiation and prime factorization, the process above is associative across any number of blocks; which is to say, the exact process described above for Bob can be done for blocks that aren't consecutive. In other words, a proof of non-inclusion between blocks 100 and 101 looks exactly the same as a proof of non-inclusion between blocks 100 and 1,000,000; both only require Bob to store a single number.
(End of math)
And if you think about it, it's a safe bet that for a given coin’s lifetime, it will most likely only be transferred occasionally; for the vast majority of Plasma blocks, it will probably sit still. With the mechanism we just covered, the intervals between coin transfers now only require constant-sized data (just a number or two); so now client-side data storage only increases with each coin transfer. This is a big deal.
Some caveats re. oversimplifications above: as described, the value of G would quickly get astronomically huge. A detail we hand-waved over is that the value has an upper bound at some modulo M; this modulo lets us restrict the growth of the accumulator value while still preserving all of the prime-factor information we need. Furthermore, however, even with this upper bound, for Alice and Bob to carry out their verification step, they would need to carry out some pretty hefty arithmetic. This, it turns out, is surmountable: there are several compact proof-schemes available that can be used, which means, in short, they can verify the result they care about without actually having to go through with the full, cumbersome computation.
There is one more unfortunate complication to address, however, which, I’m sorry to report, may not have a clean solution. Easy, lightweight proof verification is indeed something to celebrate, but let's not forget that somebody (namely, the operator) has to generate all these proofs to begin with. Calculating big stacks of compounding exponents is quite computationally expensive, certainly too much for a consumer-grade laptop to handle, for example.
Thus, at the very least, this will require the operator to have some heavier-duty server-side equipment. One hopes that we can find some way to parallelize the operations and perhaps outsource bits of the work across multiple operators, or even across the Plasma chain’s user-base. Additionally, in an odd bit of cosmic serendipity, other unrelated Ethereum-ecosystem research has lead to interest in Verifiable Delay Function ASICS, which happen to also require computing large exponent stacks and thus may be of help here. Finally, other approaches with a similar flavor to the RSA Accumulator construct, but with different mathematical/cryptographical gory details — including vector commitments and ZK-SNARK/STARK type variants — are still being explored. Whether these avenues of research ultimately yield some way to economically overcome the computational bottleneck, however, remains to be seen.
Fungible Payments: Thinking in Ranges
Finally, we’ll switch gears to alleviating the more fundamental limitation of Plasma Cash: the non-fungibility of its assets. Create a 5-Ether Plasma Cash coin, and it can't be split or merged; it remains a 5 Ether coin for its whole lifecycle.
To start thinking about how to overcome this, we can first reformulate the way we think about Plasma Cash, without actually changing any of its functionality (yet!). Let's imagine a Plasma Cash chain in which each coin represents some fixed denomination of a single asset that’s fungible on the mainchain (Ether, say). Previously, we spoke about treating each coin as a non-fungible token with a unique ID; Alice’s coin #2342 may represent exactly 20 ether. A functionality equivalent way to think about this is to imagine that all ether in the Plasma chain exists on a number line; if there’s a total of 5,000 ether on the chain, the line extends from 0 to 5,000; Alice’s 20 ether is not signified not by some unique (though otherwise arbitrary) coin ID, but instead as some segment on the number line, i.e., “the ether from 520 to 540.” To guarantee proper ownership of everyone's ether, the contract simply has to enforce that whenever a new "range" is created, it exists in an interval previously un-occupied by any other range. As long as this holds, we have a Plasma Cash model isomorphic to the old one.
So far so good — now, the upgrade: say Alice is spending her "coin," which would now mean transferring the ownership of her "range" to another party. What if, in doing so, she not only assigns the range a new owner, but alters the range’s endpoints as well? If this were possible, she would have the freedom to pay Bob a denomination of ether less than 20, i.e., "only the Ether from 520 to 523."
To accommodate this, we'll take the Plasma Cash construction and turn it sideways a bit: we'll retain this notion of "coins"; each coin will represent some bit of the number line in the smallest unit of ether we want to support (0.00001 ether, let's suppose). But now, these "coins" exist only as an abstraction — they don't, in any literal sense, make up the content of our Plasma blocks; instead, each block is now a tree of transactions, each of which spends all of the coins over a given range. If even one of the "coins" in a given range is owned by a party who is not the spender herself, the true owner can challenge, and we resolve things using the sort of cryptoeconomic challenge games familiar from Vanilla Plasma Cash.
So now, the new puzzle is this: how can Alice succinctly prove to Bob that the full range of coins she is transacting is all rightfully owned by her, and likewise, that no other transactions' ranges overlap and "bleed" into his? Unlike before, when each transaction was self contained to a single coin, we now need our proof to somehow convey information about other transactions in the block.
To get there, we introduce... yet another Merkle Tree variant! We call this new data structure a Merkle Index Tree. The leaves are the transactions themselves, each representing the transfer of a range of coins; what's new with the Merkle Index Tree is that now each node in the tree also gets a number assigned to it. The two rules are:
- The ranges of the leaves at the bottom of the tree have to be arranged consecutively (i.e., each range's ending point must be less than the next range's starting point), and;
- The numerical value of each parent node is equal to the smaller value of its two children (if its children are ranges, we use each range's starting value).
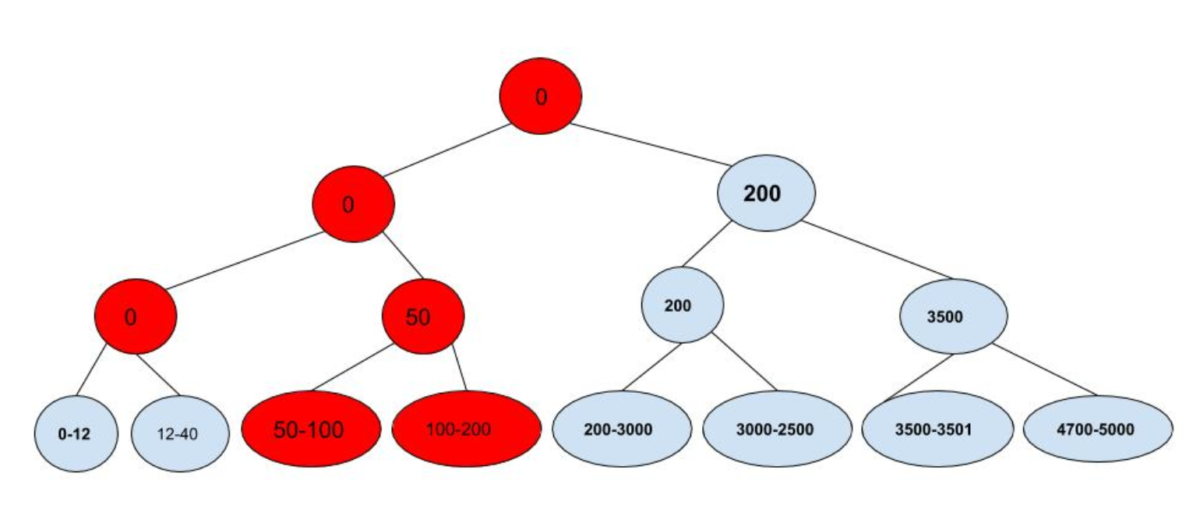
As long as a the recipient of a range verifies that the rules described above hold, a Merkle proof is enough to give them assurance that no ranges overlap the one in question. Try to break it; you can't!
So the construction above lets Alice send only a subsection of a range she owns, which lets her, in some sense, "split up" her ether. Next, we want users to be able to "merge" their ether; say Bob has a total of 12 ether, the "520 to 523" ether he received from Alice, as well as the ether in the "1001 to 1010" range. We want Bob to have the ability to send all 12 ether as a single, atomic payment.
With a bit of fancy footwork, this can be achieved: there's nothing inherently preventing a single transaction from specifying a payment multiple ranges, all of which are cancelled if any one of them is shown to be invalid. The trouble is, now the recipient needs to track the history of both ranges. And of course, if they then send all this to another party, along with some additional ranges, that party needs the history for all ranges involved. Thus, we slowly approach a terminal point of all parties needing to validate the entire chain again; the "proof size" corner of the carpet pops up.
To combat this, parties can "defragment" their ranges when the history size starts to approach problematic levels. They do this by simply swapping ranges (of equal value) with other parties so that ranges start to consolidate as much as possible; one can think of this as being analogous to channel rebalancing strategies in payment channel networks. The operator, who has a global view of the whole network, is an obvious candidate to help facilitate this. Several cryptoeconomic mechanisms and defragmentation algorithms for carrying this out have been discussed, but it likely will require testing out in the wild to see what works best.
(Note: another family of constructions — namely, hybrid channel/plasma models — can also give us, among other things, greater payment fungibility. These will be explored in part 3).
Conclusion
Congrats, you made it! So where do things stand then, Plasma-wise? Has the Plasma puzzle been cracked? Hard to say; nothing described above seems to be a silver bullet solution, which feels unsatisfying; at the same time, employing the various techniques we have in the toolkit may ultimately be enough to make a Plasma chain workable. Time will tell; in any case, the research and development flies forward at an alarming rate, so odds are, by the time you're reading this, there'll already be more things to reckon with (sorry). Until next time, best of luck.
Thanks to Ben Rose, Dan Robinson, and Georgios Konstantopolous for the helpful discussions and feedback
Author: Daniel Goldman
© 2023 The Block. All Rights Reserved. This article is provided for informational purposes only. It is not offered or intended to be used as legal, tax, investment, financial, or other advice.


