A technical perspective on Facebook’s LibraBFT Consensus algorithm

Quick Take
- The Libra blockchain will uses a robust and efficient state machine replication system called LibraBFT
- LibraBFT belongs to the class of classical BFT consensus algorithms. It is based on another consensus algorithm called HotStuff [2], which in turn borrows some of its consensus logic from yet another classical BFT algorithm called Practical Byzantine Fault Tolerance, pBFT
- LibraBFT improves upon HotStuff with a detailed specification and implementation of the Pacemaker mechanism. It also comes with a liveness analysis that consists of concrete bounds to transaction commitment

Rag Bhagavatha and Chris McCoy are the co-creators of Storecoin
Libra Blockchain overview
Facebook yesterday unveiled its new low-volatility cryptocurrency Libra, powered by a smart contract platform that’s designed to be “secure, scalable, and reliable”.

Libra Blockchain uses a robust and efficient state machine replication system called LibraBFT [1], which is the focus of this technical analysis. We discuss its properties and compare it to other Byzantine Fault Tolerant (BFT) consensus protocols with similar properties.
Classical and Nakamoto consensus
Consensus is a process used to achieve agreement on a single data value among distributed processes or systems. The processes participating in the consensus may or may not trust each other and yet, they will be able to arrive at an agreement on a single data value. There are two classes of consensus algorithms.
- Nakamoto style algorithms — This class of consensus algorithms, popularized by Bitcoin, elect a leader randomly via a cryptographic puzzle and the leader proposes a block of transactions along with a proof-of-work (PoW) to all the other processes in the network. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If the majority is controlled by honest processes, the honest chain will grow the fastest and outpace any competing chains.
- Classical consensus algorithms — In this class of algorithms, the participating processes reach consensus using multiple rounds of message exchanges carrying votes and safety-proofs. A majority of processes must agree on the votes and safety-proofs in order to achieve consensus.
Classical consensus algorithms satisfy the following general properties.
Validity — If a correct process p broadcasts a message m, then p eventually delivers m.
Agreement — If a message m is delivered by some correct process, then m is eventually delivered by every correct process.
Integrity — No correct process delivers the same message more than once; moreover, if a correct process delivers a message m and the sender p of m is correct, then m was previously broadcast by p.
Total order — For messages m1 and m2, suppose p and q are two correct processes that deliver m1 and m2. Then p delivers m1 before m2 if and only if q delivers m1 before m2.
Crash and Byzantine Failures
When a network of disparate processes participate in a consensus process, failures occur. For example, processes may crash, experience power and network failures, or simply be unable to make progress because they are stuck in a certain state. These are generally classified as crash failures. On the other hand, some processes may intentionally act maliciously to steer the consensus to their benefit. Such failures are called Byzantine failures. Consensus algorithms that tolerate Byzantine failures are called Byzantine Fault Tolerant (BFT) algorithms. BFT consensus algorithms are also capable of handling crash failures automatically.
Permissioned and Permissionless Networks
The network of processes participating in the consensus process can be configured in permissioned or permissionless setups.
- Permissioned network — In a permissioned network, the identity and the count of processes in the network are known to all processes. Thus, a process can trust the messages originating from another process in the same network. While processes may leave and join the network at will, their identities must be known apriori to all the processes in the network.
- Permissionless network — In a permissionless network, neither the process identities nor their counts are known to other processes. So, when a new process joins the network it must provide some form of proof-of-work to prove its membership to other processes.
Libra Blockchain will be configured as a permissioned network at launch with a known set of processes called Validators. This means, all Validators in the Libra network know each other’s identities.
LibraBFT, HotStuff, pBFT, and Tendermint
LibraBFT belongs to the class of classical BFT consensus algorithms. It is based on another consensus algorithm called HotStuff [2], which in turn borrows some of its consensus logic from yet another classical BFT algorithm called Practical Byzantine Fault Tolerance, pBFT [3].
Practical Byzantine Fault Tolerance
pBFT uses a system model, which assumes an asynchronous distributed system where processes are connected by a network. The network may fail to deliver messages, delay them, duplicate them, or deliver them out of order. If N is the total number of processes in the network and f is the number of faulty (including Byzantine) processes, then pBFT requires:
N ≥ 3f + 1
processes to provide tolerance against Byzantine failures.
pBFT consensus algorithm makes progress in multiple rounds, where each round accomplishes agreement on some stage in the consensus process. Fig. 1 illustrates pBFT consensus rounds, which proceed as follows.
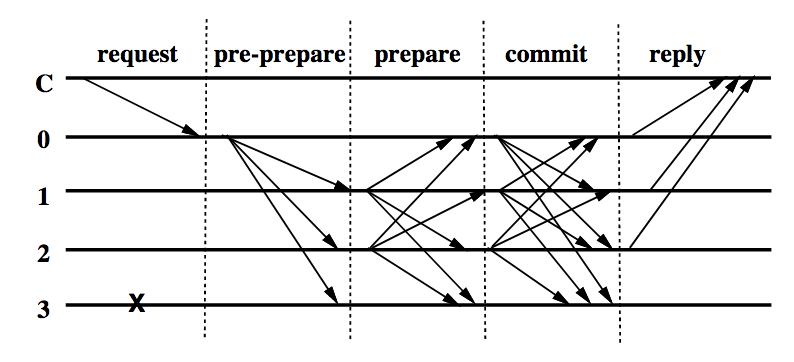
Fig. 1 — pBFT consensus rounds
- A client C sends a request to invoke a service operation to the primary process 0. This is the leader for this round of consensus.
- The primary multicasts the request to other processes, 1, 2 and 3. These processes are called replicas.
- Replicas execute the request and send a reply to the client.
- The client waits for f+1 replies from different replicas with the same result; this is the result of the operation.
The protocol makes progress and guarantees liveness, if the leader doesn’t fail. In case of leader failures, a view-change protocol is triggered after a timeout to prevent the replicas from waiting forever for messages from the leader. In a geographically distributed asynchronous network, leader failures may be more common than one can imagine, so view-change triggers may also be commonplace. So, the execution complexity of pBFT with view-changes is O(n3) where n is the number of processes in the network.
The protocol provides safety if all non-faulty replicas compute the same result. This means (N-f) processes must compute the same result and send the results to the client to guarantee safety.
HotStuff
HotStuff consensus algorithm attempts to address the O(n3) complexity of pBFT. The liveness property requires that (N−f) non-faulty replicas will run commands identically and produce the same response for each command. As is common, with the partially synchronous communication model, whereby a known bound — ∆ — on message transmission holds after some unknown global stabilization time (GST). In this model, N ≥ 3f + 1 is required for non-faulty replicas to agree on the same commands in the same order and progress can be ensured deterministically only after GST as we have discussed earlier with view-changes. HotStuff improves upon pBFT with the following two additional properties.
- Linear View Change — After GST, any correct leader, once designated, sends only O(n) authenticators to drive a consensus decision. This includes the case where a leader is replaced. Consequently, communication costs to reach consensus after GST is O(n2) authenticators in the worst case of cascading leader failures.
- Optimistic Responsiveness — After GST, any correct leader, once designated, needs to wait just for the first (N − f) responses to guarantee that it can create a proposal that will make progress. This includes the case where a leader is replaced.
Table-1 below shows the resulting improvements in the message complexity. With the correct leader, the complexity improved from O(n2) to O(n). With leader failure and the resulting view-change protocol, the complexity improved from O(n3) to O(n).
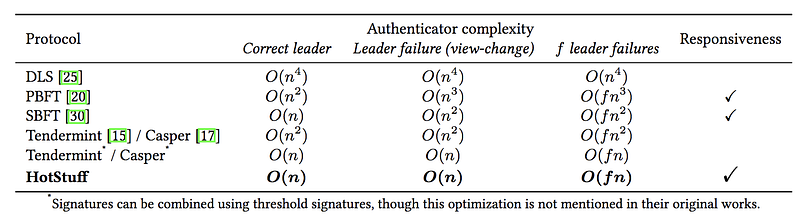
Table 1 — Comparison of message complexities of some classical BFT consensus algorithms
In pBFT each round in the consensus performs similar work (like, collecting votes from replicas etc.), which HotStuff optimizes by chaining Quorum Certificates (QC) as shown in fig. 2. With this the consensus rounds can be chained, thus improving the liveness. k view-changes requires k+2 rounds of communication instead of 2*k.
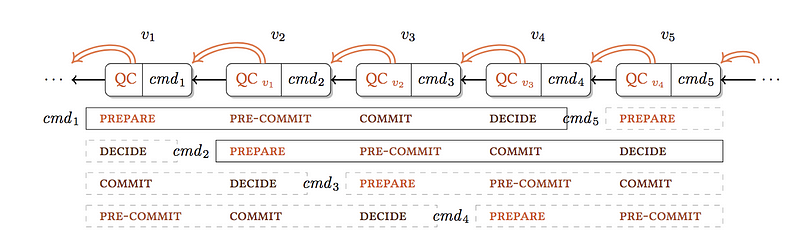
Fig. 2 — Chained HotStuff
HotStuff also implements a mechanism called Pacemaker, that guarantees liveness after GST. Pacemaker a) synchronizes all correct replicas and a unique leader into a common height for a sufficiently long period of time. It chooses the unique leader such that the correct replicas synchronized will make progress with the chosen leader. This mechanism decouples liveness from the protocol, which in turn decouples it from safety.
LibraBFT
LibraBFT improves upon HotStuff with a detailed specification and implementation of the Pacemaker mechanism discussed above. It also comes with a liveness analysis that consists of concrete bounds to transaction commitment. Other than these enhancements, LibraBFT is essentially HotStuff and makes the same assumptions about the system model with a partially synchronous network.
In LibraBFT processes are called Validators and they make progress in rounds, each having a designated validator called a leader. Leaders are responsible for proposing new blocks and obtaining signed votes from the validators on their proposals. LibraBFT follows the Chained HotStuff model described in fig. 2, which works as follows.
- A round is a communication phase with a single designated leader, and leader proposals are organized into a chain using cryptographic hashes.
- During a round, the leader proposes a block that extends the longest chain it knows.
- If the proposal is valid and timely, each honest node will sign it and send a vote back to the leader.
- After the leader has received enough votes to reach a quorum, it aggregates the votes into a Quorum Certificate (QC) that extends the same chain again.
- The QC is broadcast to every node.
- If the leader fails to assemble a QC, participants will timeout and move to the next round.
- Eventually, enough blocks and QCs will extend the chain in a timely manner, and a block will match the commit rule of the protocol.
- When this happens, the chain of uncommitted blocks up to the matching block become committed.
The above consensus process can be compared with another popular classical BFT consensus algorithm, Tendermint [4], which is illustrated in fig. 3.
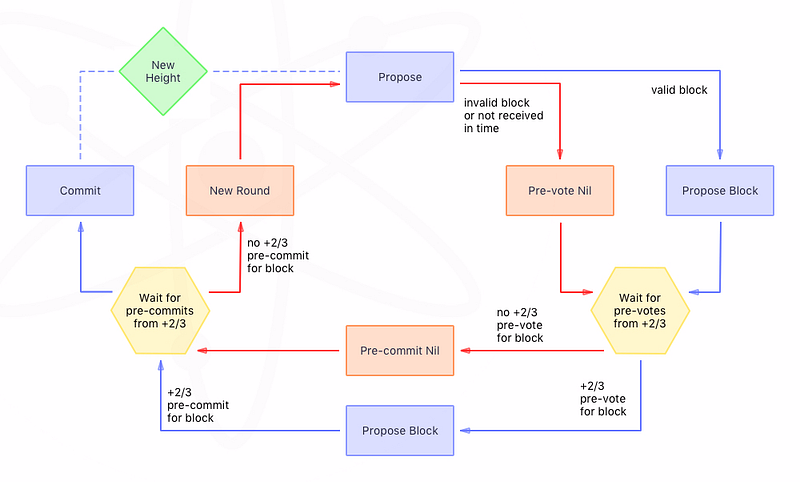
Fig. 3 — Tendermint consensus process
Like LibraBFT, Tendermint proceeds in multiple rounds — pre-vote, pre-commit, and commit — and collects Validator signatures for each round, similar to the QCs in LibraBFT. The main difference between the two algorithms is that in Tendermint each round has a timeout and the Validators wait even if they finish the round sooner whereas in LibraBFT, once the network is synchronous, the protocol speed is based on the network latency, as long as the leader is correct.
The qualification highlighted above is important. The protocol terminates without having to wait for a timeout, only if the leader is correct. If the leader fails, the view-change protocol triggers after GST and while the view-change is linear and is optimized when compared to pBFT, it may not perform any better than Tendermint’s implementation.
Practical implications of LibraBFT
Libra Blockchain is launched as a permissioned network. The founding Validators include the likes of Uber, Visa, MasterCard, PayPal, etc. Founding members are required to meet strict guidelines to be part of the early Validator set. For instance, crypto hedge funds had to have an AUM above $1 billion while digital asset-focused custodians had to store at least $100 million. Non-crypto firms needed to have a market cap of more than $1 billion or boast customer balances equaling more than $500 million. With such stringent requirements in place, one can assume that the Validators will more likely be run in data centers with private or highly reliable networking connecting them. They are likely be fault tolerant, similar to the setup required to run Cosmos Validators (which run Tendermint consensus algorithm). So practically speaking, Chained HotStuff will likely be the only important design that improves the liveness of the protocol. All other design improvements may be less useful in the practical deployment described above. On the other hand, if the network is assumed to be unreliable, the assumptions made about the correctness of leaders for fast termination may in fact fail, resulting in worst case performance.
References
- LibraBFT — https://developers.libra.org/docs/assets/papers/libra-consensus-state-machine-replication-in-the-libra-blockchain.pdf
- HotStuff BFT consensus — https://arxiv.org/pdf/1803.05069.pdf
- Practical Byzantine Fault Tolerance — http://pmg.csail.mit.edu/papers/osdi99.pdf
- Tendermint consensus algorithm — https://arxiv.org/pdf/1807.04938.pdf
© 2023 The Block. All Rights Reserved. This article is provided for informational purposes only. It is not offered or intended to be used as legal, tax, investment, financial, or other advice.